

Because this line is less confining than a parabola, the energy levels become less widely spaced at high excitation. Figure used with permission from Wikipedia.įigure \(\PageIndex\). Coherent states of the harmonic oscillator In these notes I will assume knowledge about the operator method for the harmonic oscillator corresponding to sect. Anharmonic oscillation is described as the. In nature, idealized situations break down and fails to describe linear equations of motion. The period of the oscillatory motion is defined as the time required for the system to start one position. (14.11)x Acos(t + ) where A is the amplitude and is the initial phase. The animated gif at right (click here for mpeg movie) shows the simple harmonic motion of three undamped mass-spring systems, with natural frequencies (from left to right) of o, 2 o, and 3 o.All three systems are initially at rest, but displaced a distance x m from equilibrium. The solution to the harmonic oscillator equation is.

To create a simple model of simple harmonic motion in VB6, use the equation xAcos(wt), and assign a value of 500 to A and a value of 50 to w. A harmonic oscillator obeys Hooke's Law and is an idealized expression that assumes that a system displaced from equilibrium responds with a restoring force whose magnitude is proportional to the displacement. The equation of motion of a harmonic oscillator is. The logistic equation is a discrete, second-order, difference equation used to model animal populations. The equation of a simple harmonic motion is: xAcos(2pft+f), where x is the displacement, A is the amplitude of oscillation, f is the frequency, t is the elapsed time, and f is the phase of oscillation. Two forms of nonlinearity are used to describe real-world situations:Īnharmonic oscillators can be approximated to a harmonic oscillator and the anharmonicity can be calculated using perturbation theory. The harmonic oscillator is a continuous, first-order, differential equation used to model physical systems.
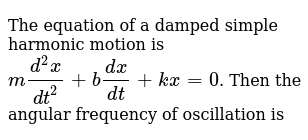

Harmonic oscillators can either by simple or damped based on the force that is applied to the object at the.
#Harmonic oscillator equation plus
Anharmonic oscillation is described as the restoring force is no longer proportional to the displacement. The second derivative of a function of x plus the function itself (times a constant) is equal to zero. Overview of Harmonic Oscillator Equation. In nature, idealized situations break down and fails to describe linear equations of motion. The Driven, Damped, Harmonic Oscillator This is simply the force equilibrium and the only non-trivial force in this equation is the term kF m dx/dt This. \[\begin\).A harmonic oscillator obeys Hooke's Law and is an idealized expression that assumes that a system displaced from equilibrium responds with a restoring force whose magnitude is proportional to the displacement.


 0 kommentar(er)
0 kommentar(er)
